Date:2025-07-18
Verlet Integration | A Stable and Natural Numerical Method for Simulating Motion
This article introduces “Verlet integration,” a numerical method essential in physics simulations. Known for its high energy conservation and smooth, stable motion reproduction, Verlet integration finds widespread use in game physics, cloth and rope simulation, and even molecular dynamics.

The full sample code for this article is available for download on Patreon after following.
(It uses openFrameworks for the implementation.)
☕ Support my Work:) / Coffee Supplier on Patreon
This guide covers the following:
- The basic concept and formula of Verlet integration
- Comparison with the Euler method
- Variants: Position Verlet, Velocity Verlet, and Leapfrog method
- Implementation examples in Processing
- Key considerations and limitations
Whether you’re a beginner or a more advanced user, this article provides a practical overview for understanding and applying Verlet integration.
1. What Is Verlet Integration?
Verlet integration is a numerical method used to compute the motion of objects over time, particularly well-suited for simulations that require energy conservation and natural dynamics. It calculates the next position based only on the current and previous positions along with the applied force.
Advantages of Verlet Integration:
- Energy Stability: Prevents artificial gain or loss of energy over time
- No Explicit Velocity Required: Simplifies calculation and leads to natural behavior
- Lightweight and Responsive: Ideal for visual art, real-time systems, and interactive environments
These features make it widely adopted in game development, generative art, and scientific simulations.
2. Mathematical Foundation
The core formula of Verlet integration updates the position based on previous and current positions:
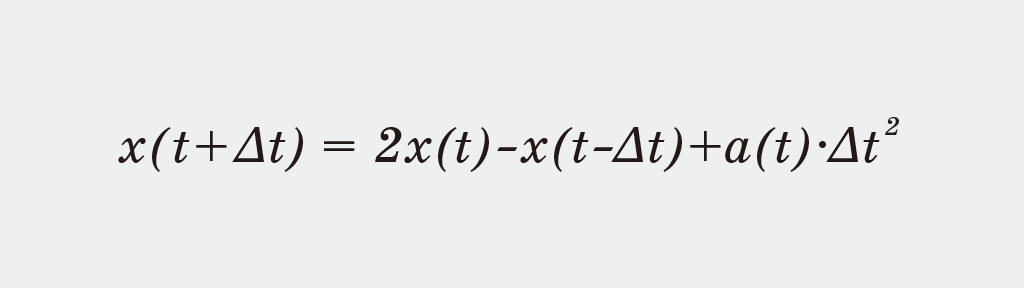
- x(t+Δt) : Position at the next time step
- x(t) : Current position
- x(t−Δt) : Previous position
- a(t) : Current acceleration
- Δt : Time step
Rather than computing future positions from velocity like in Euler’s method, Verlet uses a combination of:
- Displacement from the previous step: (x(t)−x(t−Δt))
- The influence of acceleration
This results in a natural “inertial” motion plus force-driven behavior.
3. Comparison with the Euler Method
| Feature | Euler Method | Verlet Method |
|---|---|---|
| Stability | ✗ Low (can diverge) | ✓ High (energy-conserving) |
| Simplicity | ✓ Very simple | ✗ Slightly more complex |
| Accuracy | Low | Medium to High |
| Use Cases | Prototypes | Realistic simulations |
Example: Euler can cause spring simulations to spiral out of control, while Verlet maintains natural oscillations.
4. Variants of Verlet Integration
Verlet integration has multiple variants tailored to different use cases. Here, we introduce three widely used forms, each with code examples in Processing:
Velocity Verlet (explicit velocity tracking)
Velocity Verlet is one of the most widely used time integration algorithms in molecular dynamics simulations. It explicitly maintains velocity and calculates the next velocity using the average of the current and new acceleration. This allows it to naturally handle velocity-dependent forces such as air resistance and friction. It is known for its stability and energy conservation properties, making it suitable for long-term simulations.
Formulas:
- x(t+Δt) = x(t) + v(t)Δt + 0.5·a(t)Δt²
- a(t+Δt) = F(r(t+Δt)) / m
- v(t+Δt) = v(t) + 0.5·(a(t) + a(t+Δt))Δt
Pros:
- Direct velocity access
- Highly stable and energy-conserving
- Time-reversible
Sample:
PVector position = new PVector(100, 100);
PVector velocity = new PVector(0, 0);
PVector acceleration = new PVector(0, 0.5);
void update() {
position.add(PVector.mult(velocity, 1));
position.add(PVector.mult(acceleration, 0.5)); // 0.5 * a(t) * dt^2(dt=1)
PVector newAcc = new PVector(0, 0.5);
vel.add(PVector.add(acceleration, newAcc).mult(0.5)); // v(t+1) = v(t) + 0.5*(a(t)+a(t+1))
acceleration = newAcc;
}
}
Leapfrog Method (velocity offset by half-step)
The Leapfrog method evaluates position and velocity at staggered time steps—position at integer time steps and velocity at half-integer time steps, like a “leaping frog.”
Because of this half-step offset between updates of position and velocity, Leapfrog achieves highly stable numerical integration over long periods, similar to Velocity Verlet. It is often used in game physics and particle systems.Formulas:
- v(t+Δt/2)=v(t−Δt/2)+a(t)Δt
- x(t+Δt)=x(t)+v(t+Δt/2)Δt
- a(t+Δt)=F(x(t+Δt))/m
Pros:
- High stability
- Time-reversibility
- Slightly simpler than Velocity Verlet
Cons:
- Requires handling half-step velocities
Sample:
PVector position = new PVector(100, 100);
PVector velocity = new PVector(0, 0.5);
PVector acceleration = new PVector(0, 0.5);
void update() {
velocity.add(PVector.mult(acceleration, 1)); // v(t+1/2)
position.add(velocity); // x(t+1)
acceleration = new PVector(0, 0.5);
}
Position Verlet (simplest form)
Position Verlet is the simplest form of Verlet integration. It does not store velocity explicitly but estimates the next position using only the current and previous positions. Due to its strong energy conservation characteristics, it is well-suited for simulating systems like cloth and spring dynamics.
Formulas:
- x(t+Δt) = 2x(t) − x(t−Δt) + a(t)Δt²
- a(t+Δt) = F(x(t+Δt)) / m
Pros:
- Very stable
- Time-reversible
- Compact and efficient
Cons:
- Velocity must be inferred from positions
- Requires initialization of two positions
Sample:
PVector pos = new PVector(100, 100);
PVector prevPos = pos.copy();
PVector acc = new PVector(0, 0.5);
void update() {
PVector temp = pos.copy();
PVector velocity = PVector.sub(pos, prevPos);
pos.add(velocity).add(acc); // x(t+1) = x(t) + (x(t) - x(t-1)) + a(t)
prevPos = temp;
}
Summary Table
| Variant | Uses Velocity | Accuracy | Stability | Best For |
|---|---|---|---|---|
| Velocity Verlet | Yes | High | High | Molecular dynamics, damping |
| Leapfrog | Half-step | Med-High | Very High | Game physics, particle systems |
| Position Verlet | No | Medium | High | Springs, ropes, cloth simulations |
5. Implementation Examples in Processing
Verlet integration allows for easy implementation of real-time physics visualizations.
Example code for visual implementation using Processing is available for download on Patreon.
Bouncing Ball (Position Verlet)

Cloth Simulation (Grid of Particles)
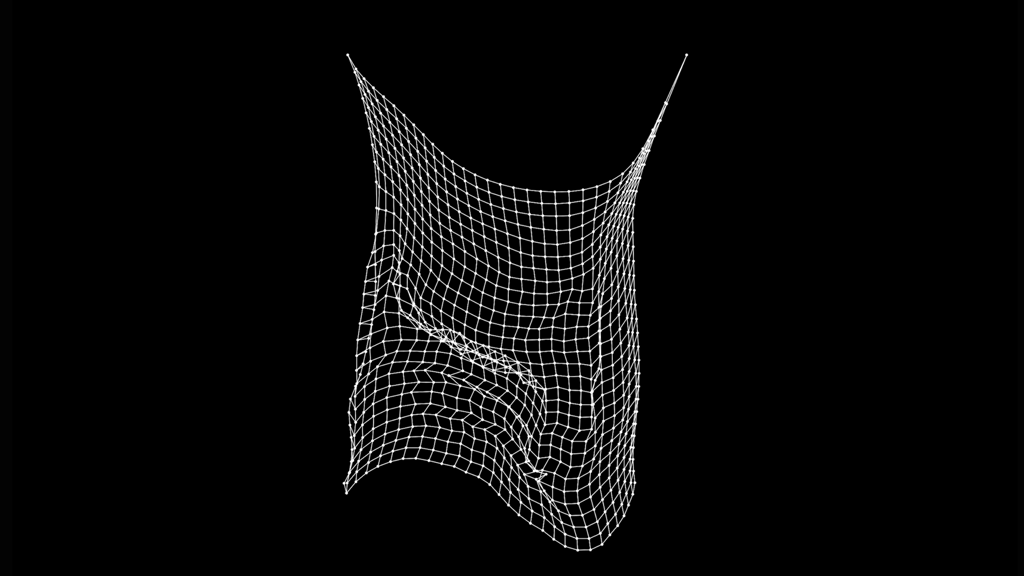
6. Limitations and Considerations
While powerful, Verlet integration has its caveats:
- No Explicit Velocity in Position Verlet:
Hard to model air resistance or friction. Use Velocity Verlet or Leapfrog when velocity matters. - Not Ideal for Rigid Constraints:
Complex rigid bodies or rotation may require constraint solvers or hybrid methods. - Numerical Stability Depends on Time Step:
LargeΔtleads to instability. Use smaller steps for high-frequency systems. - Energy Conservation May Delay Damping:
Additional damping must be introduced to stabilize behavior.
7. Verlet integration
Verlet integration is an excellent tool for simulating natural motion and oscillation. It is simple, visually expressive, and works across a wide range of applications, from generative visuals and interactive art to game physics and scientific modeling.
Reference:Wikipedia Verlet integration
Recommended Book / Generative art for beginner

Generative Art: A Practical Guide Using Processing – Matt Pearson
Generative Art presents both the techniques and the beauty of algorithmic art. In it, you’ll find dozens of high-quality examples of generative art, along with the specific steps the author followed to create each unique piece using the Processing programming language. The book includes concise tutorials for each of the technical components required to create the book’s images, and it offers countless suggestions for how you can combine and reuse the various techniques to create your own works.
Purchase of the print book comes with an offer of a free PDF, ePub, and Kindle eBook from Manning. Also available is all code from the book.
—–
► Generative Art: A Practical Guide Using Processing – Matt Pearson
Publication date: 2011. July
Support my Website
By using our affiliate links, you’re helping my content and allows me to keep creating valuable articles. I appreciate it so much:)
BGD_SOUNDS (barbe_generative_diary SOUNDS)
barbe_generative_diary SOUNDS will start sharing and selling a variety of field recordings collected for use in my artwork “Sound Visualization” experiments. All sounds are royalty-free.



