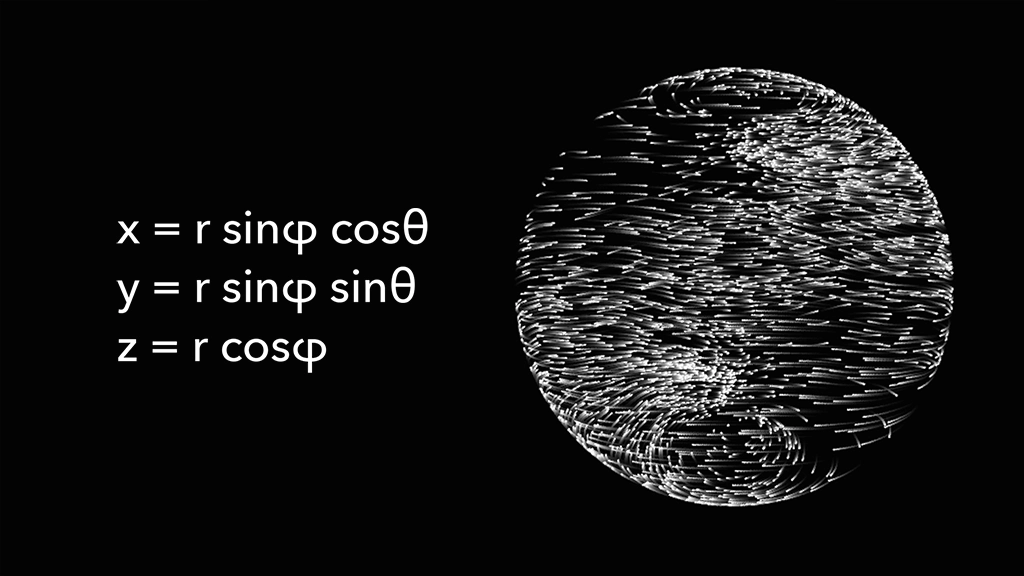
The Particles on a spherical surface Code

This code is for particles moving as if flowing on a spherical surface. It utilizes the spherical coordinate system to obtain the positions of the points.

int ParticleCount = 3000;
float radius = 200;
float noiseNum;
Particle[] Particles = new Particle[ParticleCount];

void setup(){
 size(1300,1300,P3D);
 for(int i = 0; i < ParticleCount; i++) {
    Particles[i] = new Particle();
  }
}

void draw(){
  fill(0,20);
  noStroke();
  rect(0,0,width,height);
  translate(width/2,height/2,radius);
  rotateX(PI*0.25);
  //rotateX(frameCount*0.001);
  //rotateY(frameCount*0.003);
  //rotateZ(frameCount*0.002);

  for(int i = 0; i < ParticleCount; i++){
    Particles[i].update();
  }
}

class Particle{
  PVector p;
  float ranCos, radNum;
  float noiseScale = 0.01; 

  Particle(){
    ranCos = random(-1, 1);
    radNum = radians(random(360));
    float xPos = radius * sqrt(1 - pow(ranCos,2)) * cos(radNum);
    float yPos = radius * sqrt(1 - pow(ranCos,2)) * sin(radNum);
    float zPos = radius * ranCos;
    p = new PVector(xPos, yPos, zPos);
  }
  
  void update(){
    noiseDetail(3,0.65);
    noiseNum = noise(p.x*noiseScale, p.y*noiseScale, p.z*noiseScale) * 0.01;
      
    float sign = 0;
    if (p.y > 0){sign = 1;}
    if (p.y < 0){sign = -1;}  
    float aCos = acos(p.z / sqrt(pow(p.x, 2) + pow(p.y,2)+pow(p.z,2)));
    float signAcos = sign * acos(p.x / sqrt(pow(p.x,2)+pow(p.y,2)))+noiseNum;
    
    p.x = radius * sin(aCos) * cos(signAcos);
    p.y = radius * sin(aCos) * sin(signAcos);
    p.z = radius * cos(aCos) + cos(signAcos)*1.2;
    
    stroke(255);
    strokeWeight(2);
    point(p.x, p.y, p.z);
  }
}

Samples

View this post on Instagram

A post shared by bgd peco (@barbe_generative_diary)

Recommends

generative art / a practical guide using processing

I always recommend this book, whenever I am asked by a beginner, “How do you make your work?”. The book includes high-quality examples of generative art.

https://barbegenerativediary.com/en/gear-and-tools/generative-art-a-practical-guide-using-processing/