TOP
Tutorials
Processing / Tutorials
Error Diffusion（Floyd–Steinberg / Atkinson）in Processing : From Basics to Levels

Processing / Tutorials

Date:2026-02-13

Error Diffusion（Floyd–Steinberg / Atkinson）in Processing : From Basics to Levels

Error diffusion（誤差拡散）は、量子化誤差を周囲へ分配しながら処理することで、少ない階調でも滑らかな明るさを表現するディザリング手法です。閾値行列方式とは異なり、結果はより自然なノイズ状の質感になりやすいのが特徴です。

Error Diffusion_Floyd–Steinberg Atkinson-header

ディザリング（Dithering）は、少ない色数や階調しか扱えない環境で、画像をより滑らかに見せるための古典的な画像処理技術です。前回の記事では、ディザリングの中でも最も基本的な Ordered dithering（規則ディザ） を取り上げ、Bayer行列を用いた実装をProcessingで行いました。

本記事では、ディザリングのもう一つの柱である Error diffusion を扱います。特に代表的な方式である Floyd–Steinberg と、アート表現でも人気の高い Atkinson をProcessingで実装し、Ordered ditheringとの違いまで整理します。

この記事の完全なサンプルコードは、Patreonからダウンロードできます。
☕ Coffee Supplier on Patreon

1. Error diffusion（誤差拡散）とは何か？

Error diffusion（誤差拡散）は、ディザリングの中でも「誤差を伝播させる」ことで階調を表現する方式です。

白黒2値化のような量子化では、各ピクセルの明るさは最終的に

0（黒）
255（白）

のどちらかに丸められます。しかしこの丸め処理では、必ず 誤差（error） が発生します。

たとえば、元の明るさが 180 だった場合、

白に丸めると 255
誤差は 180 – 255 = -75

となります。誤差拡散は、この誤差を捨てずに 周囲の未処理ピクセルへ分配し、全体として元画像に近い明るさを保つように補正します。

2. Ordered dithering との違い

前回扱った Ordered dithering は、

位置ごとに閾値を変える
閾値マップ（Bayer行列）をタイル状に繰り返す

という方式でした。

一方で誤差拡散は、

閾値マップを使わない
各ピクセルの処理結果が、次のピクセルへ影響する

という性質を持ちます。

そのため、結果として現れる粒は規則模様ではなく、より自然なノイズ状になります。

ただし副作用として、動画やリアルタイム描画では粒がフレームごとに変化しやすく、Ordered ditheringよりも「わらわら動く」印象が出やすい傾向があります。

3. 誤差拡散の基本手順

誤差拡散のアルゴリズムは、基本的に次の流れです。

元画像の明るさを取得する
そのピクセルを量子化（2値化、または少階調化）する
誤差（元 – 量子化後）を計算する
誤差を周囲の未処理ピクセルへ加算する
次のピクセルへ進む

このとき重要なのは、「誤差を加算した結果」を保持するために 作業用バッファ（配列） を持つことです。

Processingの pixels[] に直接誤差を加算していくと、色形式や型変換が混ざって扱いづらいため、明るさだけを float[] として保持するのが最もシンプルです。

4. Floyd–Steinberg法とは？

誤差拡散の中で最も有名で、基本となる方式が Floyd–Steinberg dithering です。

Floyd–Steinbergでは、誤差を次の4方向へ決まった比率で分配します。

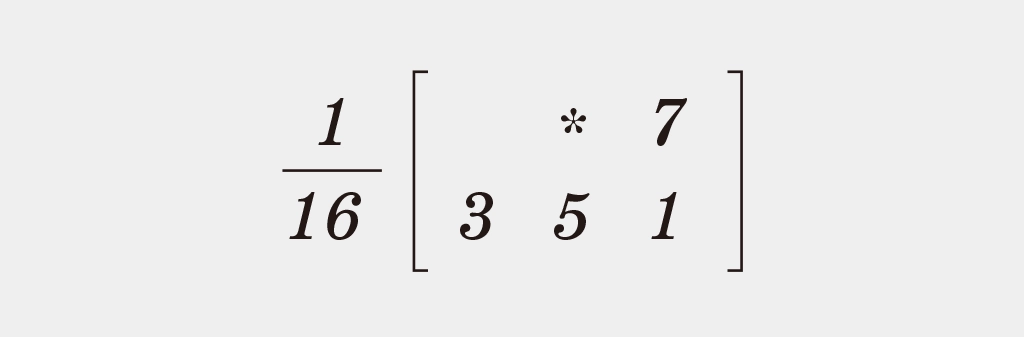
右 : 7/16
左下 : 3/16
下 : 5/16
右下 : 1/16

という比率で誤差を配ります。この方式は階調表現が強く、写真のような画像にも向いています。

5. Processingでの実装（Floyd–Steinberg / 2値）

以下は最小構成のFloyd–Steinberg実装例です。
（前回記事と同様に「Processingで動く形」を優先し、構造を分かりやすくしています）


void applyFloydSteinberg(PGraphics source) {
  loadPixels();
  source.loadPixels();

  int w = width;
  int h = height;

  // 作業用の明るさバッファ（誤差を加算していく）
  float[] buf = new float[w * h];

  for (int i = 0; i < buf.length; i++) {
    buf[i] = brightness(source.pixels[i]); // 0..255
  }

  for (int y = 0; y < h; y++) {
    for (int x = 0; x < w; x++) {
      int loc = x + y * w;

      float oldV = buf[loc];
      float newV = (oldV < 128) ? 0 : 255;

      pixels[loc] = color(newV);

      float err = oldV - newV;

      // 誤差拡散（配列外チェックつき）
      addError(buf, x + 1, y,     w, h, err * 7.0/16.0);
      addError(buf, x - 1, y + 1, w, h, err * 3.0/16.0);
      addError(buf, x,     y + 1, w, h, err * 5.0/16.0);
      addError(buf, x + 1, y + 1, w, h, err * 1.0/16.0);
    }
  }

  updatePixels();
}

void addError(float[] buf, int x, int y, int w, int h, float v) {
  if (x < 0 || x >= w || y < 0 || y >= h) return;
  int loc = x + y * w;
  buf[loc] = constrain(buf[loc] + v, 0, 255);
}

6. このコードで起きていること（誤差の意味）

この実装で重要なのは、次の2行です。


float err = oldV - newV;
addError(..., err * ratio);

oldV は、誤差を含んだ現在の明るさ
newV は、最終的に黒か白へ丸めた値

この差分 err が、量子化によって失われた情報です。Floyd–Steinbergは、この失われた情報を周囲へ配ることで、全体として元画像に近い明るさが維持されるように働きます。

7. Atkinson法とは？

Atkinson dithering は、誤差拡散の中でも特にアート表現で人気のある方式です。

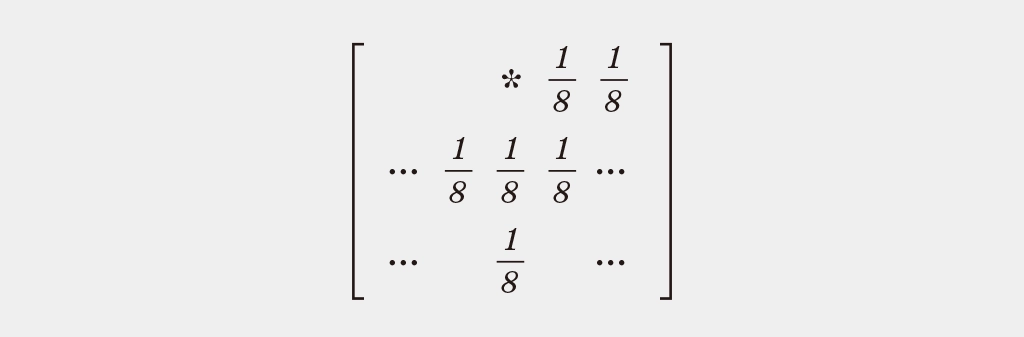
Atkinsonでは誤差を次の6方向へ、均等に（1/8ずつ）分配します。

右（x+1, y）
右2つ（x+2, y）
左下（x-1, y+1）
下（x, y+1）
右下（x+1, y+1）
2つ下（x, y+2）

Floyd–Steinbergよりも粒が軽く、やや「印刷物」「グラフィック」寄りの印象が出やすいのが特徴です。

8. Processingでの実装（Atkinson / 2値）


void applyAtkinson(PGraphics source) {
  loadPixels();
  source.loadPixels();

  int w = width;
  int h = height;

  float[] buf = new float[w * h];
  for (int i = 0; i < buf.length; i++) {
    buf[i] = brightness(source.pixels[i]); // 0..255
  }

  for (int y = 0; y < h; y++) {
    for (int x = 0; x < w; x++) {
      int loc = x + y * w;

      float oldV = buf[loc];
      float newV = (oldV < 128) ? 0 : 255;

      pixels[loc] = color(newV);

      float err = oldV - newV;
      float e = err / 8.0;

      addError(buf, x + 1, y,     w, h, e);
      addError(buf, x + 2, y,     w, h, e);
      addError(buf, x - 1, y + 1, w, h, e);
      addError(buf, x,     y + 1, w, h, e);
      addError(buf, x + 1, y + 1, w, h, e);
      addError(buf, x,     y + 2, w, h, e);
    }
  }

  updatePixels();
}

9. Floyd–Steinberg と Atkinson の違い

両者はどちらも誤差拡散ですが、分配の仕方が異なるため見た目の傾向が変わります。

Floyd–Steinberg

階調表現が強い
粒が細かく、写真向き
暗部も残りやすい

Atkinson

粒が軽く、グラフィック向き
コントラストが出やすい
画像が少し「整理された」印象になりやすい

10. levels（階調数）への拡張

ここまでの実装は、出力が黒 or 白の2値に固定されていました。しかし誤差拡散も、Ordered ditheringと同様に少階調へ拡張できます。levels は「量子化の段数（出力できる明るさの数）」を意味します。

levels = 2 → 2値（0 / 255）
levels = 4 → 4階調（0 / 85 / 170 / 255）
levels = 8 → 8階調
levels = 16 → 16階調

誤差拡散においても本質は同じで、量子化によって失われた誤差を周囲へ分配するという構造を保ったまま、量子化の部分だけを「多段階」に置き換えます。

11. Processingでの実装（levels対応版）

以下は、Floyd–SteinbergとAtkinsonを levels 対応に拡張した実装例です。

量子化関数（0..255 → levels段階へ丸める）


float quantizeLevels(float v, int levels) {
  float step = 255.0 / (levels - 1);
  return round(v / step) * step;
}

Floyd–Steinberg（levels版）


void applyFloydSteinbergLevels(PGraphics source, int levels) {
  if (levels < 2) return;

  loadPixels();
  source.loadPixels();

  int w = width;
  int h = height;

  float[] buf = new float[w * h];
  for (int i = 0; i < buf.length; i++) {
    buf[i] = brightness(source.pixels[i]); // 0..255
  }

  for (int y = 0; y < h; y++) {
    for (int x = 0; x < w; x++) {
      int loc = x + y * w;

      float oldV = buf[loc];
      float newV = quantizeLevels(oldV, levels);

      pixels[loc] = color(newV);

      float err = oldV - newV;

      addError(buf, x + 1, y,     w, h, err * 7.0/16.0);
      addError(buf, x - 1, y + 1, w, h, err * 3.0/16.0);
      addError(buf, x,     y + 1, w, h, err * 5.0/16.0);
      addError(buf, x + 1, y + 1, w, h, err * 1.0/16.0);
    }
  }

  updatePixels();
}

Atkinson（levels版）


void applyAtkinsonLevels(PGraphics source, int levels) {
  if (levels < 2) return;

  loadPixels();
  source.loadPixels();

  int w = width;
  int h = height;

  float[] buf = new float[w * h];
  for (int i = 0; i < buf.length; i++) {
    buf[i] = brightness(source.pixels[i]); // 0..255
  }

  for (int y = 0; y < h; y++) {
    for (int x = 0; x < w; x++) {
      int loc = x + y * w;

      float oldV = buf[loc];
      float newV = quantizeLevels(oldV, levels);

      pixels[loc] = color(newV);

      float err = oldV - newV;
      float e = err / 8.0;

      addError(buf, x + 1, y,     w, h, e);
      addError(buf, x + 2, y,     w, h, e);
      addError(buf, x - 1, y + 1, w, h, e);
      addError(buf, x,     y + 1, w, h, e);
      addError(buf, x + 1, y + 1, w, h, e);
      addError(buf, x,     y + 2, w, h, e);
    }
  }

  updatePixels();
}

12. Ordered dithering と Error diffusion の使い分け

実用上の目安としては次のようになります。

動画やリアルタイム用途で安定性を重視する → Ordered dithering
写真のような階調を重視する → Floyd–Steinberg
グラフィック的な質感を作りたい → Atkinson

Processingで作品制作を行う場合、ディザリングは「画像処理」だけでなく「質感生成」として扱えるため、Atkinsonのような方式は特に有効です。

13. Error diffusion

本記事では、ディザリングのもう一つの柱である Error diffusion（誤差拡散） を扱い、Processingで実装しました。

Error diffusionは、量子化誤差を周囲へ分配して階調を表現する
Floyd–Steinbergは階調表現が強く、写真に向く
Atkinsonは粒が軽く、グラフィック表現に向く
誤差拡散はOrdered ditheringより粒が揺れやすい
levels拡張により少階調表現にも対応できる

14. 作品例｜Sound visualization

View this post on Instagram

A post shared by bgd peco (@barbe_generative_diary)

Recommended Book / barbe_generative_library

Grid systems in graphic design – Josef Müller-Brockmann

グリッドシステムとは。

グリッドシステムとは、連続した行と列に基づいてテキストやイメージを配置しデザインの整合性と視認性を高めるレイアウト手法です。元々は印刷レイアウトのために考えられたものですが、現在ではWebデザインなど、あらゆるデザイン設計において利用され、ProcessingやP5jsなど２Dでグラフィックを制作する場合にも、このグリッドシステムから学べる事は多い。

ーーーーー
► 『Grid systems in graphic design 』（Josef Müller-Brockmann）

1981年に刊行された完全日本語訳版。
初版／ 2019.11.9
ページ数／184ページ
出版社／ボーンデジタル
言語／日本語

BGD_SOUNDS on bandcamp

BGD_SOUNDSでは、アートワークで使用するために録音された様々な音を公開しています。

Link / BGD_SOUNDS on bandcamp

安価で利用できる膨大な著作権フリーのサウンドライブラリーを目指し、定期的に音源ライブラリーを増やしています。音源のほとんどは、192kHzの32bitにて録音。音楽制作や映像制作など、それぞれの用途に合わせて利用できます。（メタデータも含まれています。）

BGD_CLUB（月額サブスクリプション）では、低価格からすべてのライブラリーにアクセスし自由にダウンロードすることが可能です。