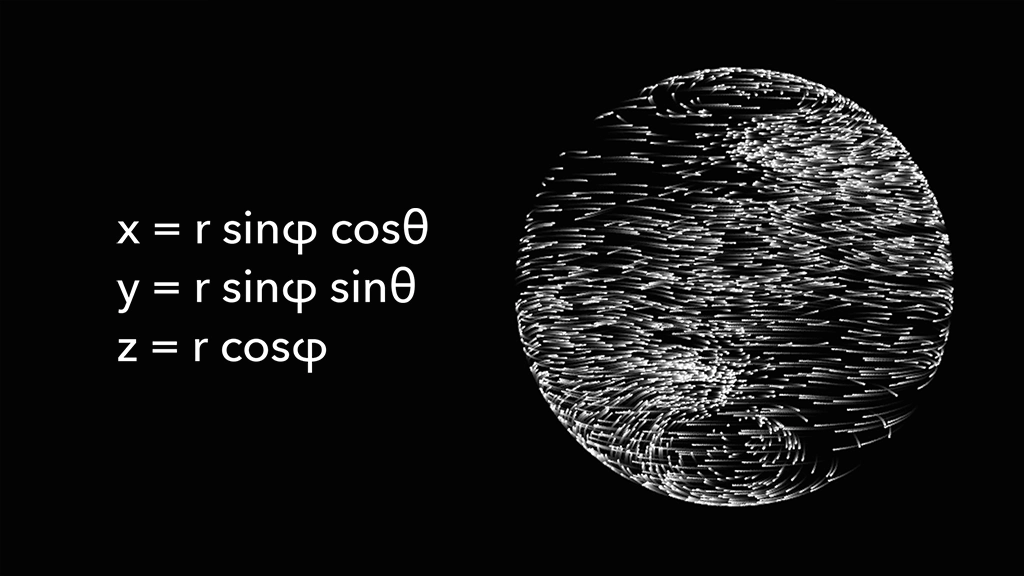
This code is for particles moving as if flowing on a spherical surface. It utilizes the spherical coordinate system to obtain the positions of the points.

The Particles on a spherical surface Code


int ParticleCount = 3000;
float radius = 200;
float noiseNum;
Particle[] Particles = new Particle[ParticleCount];

void setup(){
 size(1300,1300,P3D);
 for(int i = 0; i < ParticleCount; i++) {
    Particles[i] = new Particle();
  }
}

void draw(){
  fill(0,20);
  noStroke();
  rect(0,0,width,height);
  translate(width/2,height/2,radius);
  rotateX(PI*0.25);
  //rotateX(frameCount*0.001);
  //rotateY(frameCount*0.003);
  //rotateZ(frameCount*0.002);

  for(int i = 0; i < ParticleCount; i++){
    Particles[i].update();
  }
}

class Particle{
  PVector p;
  float ranCos, radNum;
  float noiseScale = 0.01; 

  Particle(){
    ranCos = random(-1, 1);
    radNum = radians(random(360));
    float xPos = radius * sqrt(1 - pow(ranCos,2)) * cos(radNum);
    float yPos = radius * sqrt(1 - pow(ranCos,2)) * sin(radNum);
    float zPos = radius * ranCos;
    p = new PVector(xPos, yPos, zPos);
  }
  
  void update(){
    noiseDetail(3,0.65);
    noiseNum = noise(p.x*noiseScale, p.y*noiseScale, p.z*noiseScale) * 0.01;
      
    float sign = 0;
    if (p.y > 0){sign = 1;}
    if (p.y < 0){sign = -1;}  
    float aCos = acos(p.z / sqrt(pow(p.x, 2) + pow(p.y,2)+pow(p.z,2)));
    float signAcos = sign * acos(p.x / sqrt(pow(p.x,2)+pow(p.y,2)))+noiseNum;
    
    p.x = radius * sin(aCos) * cos(signAcos);
    p.y = radius * sin(aCos) * sin(signAcos);
    p.z = radius * cos(aCos) + cos(signAcos)*1.2;
    
    stroke(255);
    strokeWeight(2);
    point(p.x, p.y, p.z);
  }
}

Samples

particles_on_a_spherical_surfaceo02

barbe_generative_library

Processing 参考書籍
[Generative art のすすめ、ビギナーのためのProcessing 入門書３冊

ジェネラティブアートが注目される中、やってみたいけどどこから始めて良いのかわからないとの相談がよくあります。多種多様なジェネラティブアート作り方中で一番分かりやすいProcessingをベースとした入門書３冊を紹介。

https://barbegenerativediary.com/books/generative-art-beginner-books3/

generative-books3