本記事の内容は以下

• Verlet integrationの基本的な考え方と数式
• オイラー法との違いと比較
• 代表的な派生形式（Position Verlet、Velocity Verlet、Leapfrog法）の紹介
• Processingによるシンプルな物理表現の実装例
• 注意点と限界

初学者から応用者まで、実践的に使える知識として整理しています。

1. Verlet integrationとは？

Verlet integrationは、物体の運動を数値的に解くための手法のひとつで、特に「エネルギー保存性」や「自然な動きの再現」に優れた特徴を持っています。位置と加速度のみに基づいて次の状態を計算するため、バネや布のような連続的で柔らかな運動を持つ構造体のシミュレーションに向いています。

主な利点：

• エネルギーが過剰に増減しない：長時間のシミュレーションでも安定した動作
• 速度の概念を持たない構造：計算がシンプルで物理的に自然な挙動になる
• ビジュアル作品やリアルタイム処理に最適：軽量で応答性が高い

これらの特徴により、ゲーム物理、アート作品、科学シミュレーションなど、幅広い応用で使われています。

2. Verlet integrationの数学的基礎

Verlet integrationは、以下のような形式で未来の位置を決定します：

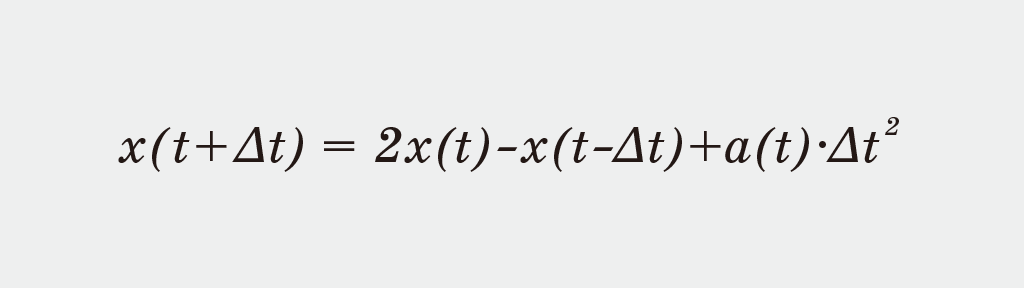
• 速度を明示的に使わず、位置と加速度で更新
• 加速度 a(t)は、F=maに基づく

各項の意味と役割

1. x(t+Δt)：次の時間ステップにおける位置（これを計算する）
2. x(t)：現在の位置
3. x(t−Δt)：１ステップ前（過去）の位置
4. a(t)：現在の加速度（外力 ÷ 質量）
5. Δt：時間ステップ幅（例えば毎フレームの秒数）

この式は、速度を明示的に使わず、過去の位置と現在の位置の差分から“見かけの速度”を求め、それを使って位置を更新する方法です。

長時間のシミュレーションにおいて、オイラー法よりも安定性が高くなります。オイラー法では現在の速度から次の位置を決めますが、Verlet法では下記のように運動の「自然な慣性」＋「力の影響」の２つで成り立っています。

• (x(t)−x(t−Δt))が「前回からの移動量」＝見かけの速度
• それに加速度（＝力の影響）を加えて、次の位置を予測

3. オイラー法との比較

特徴	オイラー法	Verlet法
安定性	△（発散しやすい）	◎（エネルギー保存に優れる）
実装の容易さ	◎（簡単）	△（前フレームの情報が必要）
精度	低	中〜高
用途	初学者、簡易表現	実用シミュレーション、ゲーム

例：オイラー法でバネをシミュレートすると数秒で不安定になりますが、Verletなら自然な振動を保ちます。

4. Verletのバリエーション

Verlet integrationにはいくつかの派生形式があり、それぞれ位置や速度の扱い方に違いがあります。目的や計算精度、安定性の観点から適切なバリエーションを選ぶことが重要です。以下では3つの代表的な形式です。

Velocity Verlet（速度を明示的に保持）

Velocity Verletは、分子動力学シミュレーションで最も広く使われている時間積分アルゴリズムの一つです。速度を明示的に管理しつつ、加速度の平均を使って次の速度を計算します。そのため、空気抵抗や摩擦のように速度依存の力も自然に扱えます。また、安定性とエネルギー保存性に優れ、長時間のシミュレーションに適しています。

Formulas:

1. x(t+Δt) = x(t) + v(t)Δt + 0.5·a(t)Δt²
2. a(t+Δt) = F(r(t+Δt)) / m
3. v(t+Δt) = v(t) + 0.5·(a(t) + a(t+Δt))Δt

Pros:

• 速度が明示的に得られる: 運動エネルギー計算や速度依存の力（空気抵抗など）の適用が容易。
• 安定性とエネルギー保存性: 長時間のシミュレーションでもエネルギーが保存される。
• 時間可逆性: 物理法則に整合している。

Cons:

• 実装がLeapfrog（次に紹介）よりわずかに複雑になる場合がある。

Processingでの簡略コード例

PVector position = new PVector(100, 100);     // 現在位置
PVector velocity = new PVector(0, 0);         // 速度
PVector acceleration = new PVector(0, 0.5);       // 加速度

void update() {
  position.add(PVector.mult(velocity, 1));                 // v(t)で位置を更新
  position.add(PVector.mult(acceleration, 0.5));               // 0.5 * a(t) * dt^2（dt=1とする）
  PVector newAcc = new PVector(0, 0.5);          // 次ステップの加速度（ここでは定数）
  vel.add(PVector.add(acceleration, newAcc).mult(0.5));   // v(t+1) = v(t) + 0.5*(a(t)+a(t+1))
  acceleration = newAcc;
}

Leapfrog法（速度と位置を半ステップずらす）

Leapfrog（リープフロッグ）法は、「カエル跳び」のように位置と速度を異なる時間点で（位置は整数タイムステップ、速度は半整数タイムステップで）評価する方法です。

速度と位置の更新タイミングが半ステップずれており、Velocity Verletと同様、長期的に非常に安定な数値解を得ることができます。主にゲームの物理シミュレーションや粒子系などで用いられます。

Formulas:

1. v(t+Δt/2)=v(t−Δt/2)+a(t)Δt
2. x(t+Δt)=x(t)+v(t+Δt/2)Δt
3. a(t+Δt)=F(x(t+Δt)​)/m

Pros:

• 安定性とエネルギー保存性: Velocity Verletと同等の優れた特性を持つ。
• 時間可逆性: 物理法則に整合している。
• 実装が比較的シンプル。

Cons:

• 速度が半整数タイムステップで得られるため、整数タイムステップでの速度が必要な場合は近似が必要になる。
• 初期化がVelocity Verlet法よりわずかに複雑。（v(-Δt/2)が必要）。

Processingでの簡略コード例:

PVector position = new PVector(100, 100);     // 現在位置
PVector velocity = new PVector(0, 0.5);       // 速度（半ステップずれ）
PVector acceleration = new PVector(0, 0.5);       // 加速度

void update() {
  velocity.add(PVector.mult(acceleration, 1));         // v(t+1/2)
  position.add(velocity);                          // x(t+1)
  acceleration = new PVector(0, 0.5);             // 加速度更新（ここでは一定）
}

Position Verlet（もっとも基本的な形式）

Position Verletは、Verlet integrationの中で最も基本的な形式です。Position Verletは、速度を保持せず、現在の位置と1つ前の時刻の位置情報から次の位置を推定する最もシンプルな形式です。エネルギー保存性が高く、布やバネのシミュレーションに適しています。

Formulas:

1. x(t+Δt) = 2x(t) − x(t−Δt) + a(t)Δt²
2. a(t+Δt) = F(x(t+Δt)) / m​

Pros:

• 安定性とエネルギー保存性: 非常に高い安定性でエネルギーを保存。
• 時間可逆性: 物理法則に整合している。
• 更新式がシンプル。

Cons:

• 速度が陽に得られない: 運動エネルギー計算や速度依存の力、衝突時の挙動処理が複雑になります。
• 初期化が複雑: r(-Δt) を推定して与える必要があります。

以下のコードはProcessingでの簡略化された実装例：

PVector pos = new PVector(100, 100);         // 現在位置
PVector prevPos = pos.copy();                // 前回の位置
PVector acc = new PVector(0, 0.5);           // 加速度

void update() {
  PVector temp = pos.copy();                 // 現在の位置を一時保存
  PVector velocity = PVector.sub(pos, prevPos);  // 現在位置と前回位置から見かけの速度
  pos.add(velocity).add(acc);               // x(t+1) = x(t) + (x(t) - x(t-1)) + a(t)
  prevPos = temp;                            // 前回位置を更新
}

比較表：各Verletバリエーションの特性

手法	速度を使う	精度	安定性	適用例
Velocity Verlet	○（計算により保持）	高	高	分子動力学、空気抵抗付き物体
Leapfrog	○（半ステップずらす）	中〜高	非常に高	ゲーム物理、粒子システム
Position Verlet	×（差分で近似）	中	高	バネ、布、ロープ

5. Processingでの実装例

Verlet integrationは、リアルタイム物理演算ビジュアルを簡単に実装できます。
以下、Processingによるビジュアルコード実装例は、Patreonにてダウンロードできます。

自由落下と反射（Position Verlet）

sample_1_PositonVerlet

布のような構造（Cloth Simulation）

sample_2_ClothSimulation

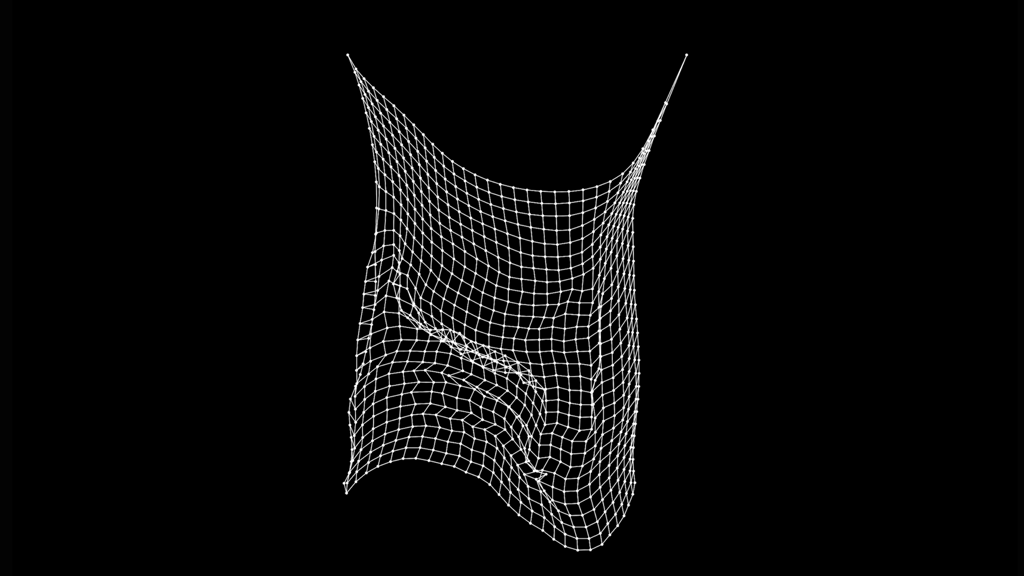
6. 注意点と限界

• 速度が明示的に得られない（Position Verlet）
  空気抵抗や摩擦など速度依存の力を加えるのが難しい。→ Velocity VerletやLeapfrogで対処
• 初期化が必要：最初の2ステップ分の位置（現在と１つ前）が必要
• 剛体や回転には拡張が必要：剛体表現やトルクなどは別途考慮が必要

7. Verlet integration

Verlet integrationは、シンプルながらも安定性と精度を兼ね備えた強力な手法です。特に布やバネのような柔軟な構造、粒子系の物理表現で大きな力を発揮します。

代表的なバリエーション（Position Verlet、Velocity Verlet、Leapfrog）を理解し、目的に応じて使い分けることで、より自然で信頼性のあるシミュレーションが可能になります。

参考：Wikipedia Verlet integration

Recommended Book / barbe_generative_library

Grid systems in graphic design – Josef Müller-Brockmann

グリッドシステムとは。

グリッドシステムとは、連続した行と列に基づいてテキストやイメージを配置しデザインの整合性と視認性を高めるレイアウト手法です。元々は印刷レイアウトのために考えられたものですが、現在ではWebデザインなど、あらゆるデザイン設計において利用され、ProcessingやP5jsなど２Dでグラフィックを制作する場合にも、このグリッドシステムから学べる事は多い。

ーーーーー
► 『Grid systems in graphic design 』（Josef Müller-Brockmann）

1981年に刊行された完全日本語訳版。
初版／ 2019.11.9
ページ数／184ページ
出版社／ボーンデジタル
言語／日本語

BGD_SOUNDS on bandcamp

BGD_SOUNDSでは、アートワークで使用するために録音された様々な音を公開しています。

Link / BGD_SOUNDS on bandcamp

安価で利用できる膨大な著作権フリーのサウンドライブラリーを目指し、定期的に音源ライブラリーを増やしています。音源のほとんどは、192kHzの32bitにて録音。音楽制作や映像制作など、それぞれの用途に合わせて利用できます。（メタデータも含まれています。）

BGD_CLUB（月額サブスクリプション）では、低価格からすべてのライブラリーにアクセスし自由にダウンロードすることが可能です。